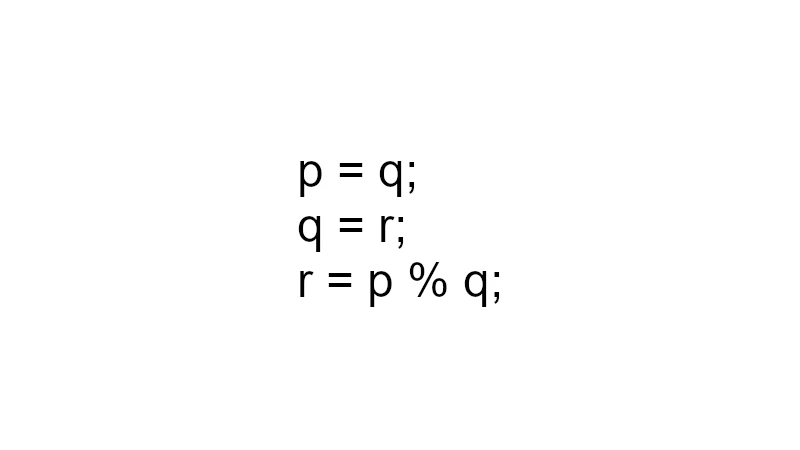こんにちは。今回はユークリッドの互除法というアルゴリズムを扱います。これは与えられた2つの自然数の最大公約数を求めるアルゴリズムです。この記事では、Javaのdo-while文を使って、このアルゴリズムを実装しました。また、Listを使って、途中経過を保持して後でまとめて出力することをしました。
ユークリッドの互除法の簡単な説明
2つの自然数をpとqとします。単純化のため、p ≥ qと仮定します。以下の手順でpとqの最大公約数を求めることができます。
- Step1:
- pをqで割った余りをrとする。
- Step2:
- rが0より大きいならば、qとrをそれぞれpとqと置き換え、Step1に戻る。
- rが0ならば、処理を終える。このときのqが求める最大公約数。(最初の段階のpとqの最大公約数。)
上記がユークリッドの互除法です。
例えば、15と21の最大公約数を求めたいとします。
上記手順におけるp, q, rの値は次のようになります。
| p | q | r | |
|---|---|---|---|
| 割り算1回目 | 21 | 15 | 6 |
| 割り算2回目 | 15 | 6 | 3 |
| 割り算3回目 | 6 | 3 | 0 |
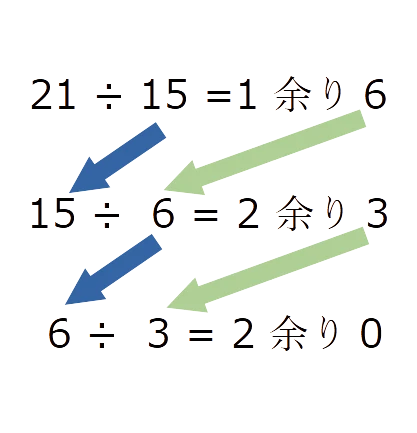
割り算3回目で余りが0になりました。その時の商が3なので、15と21の最大公約数は3です。
図形による直感的な例え:以下のように長辺p、短辺qの長方形を正方形で埋めていくと最大公約数が求まるという仕組みです。
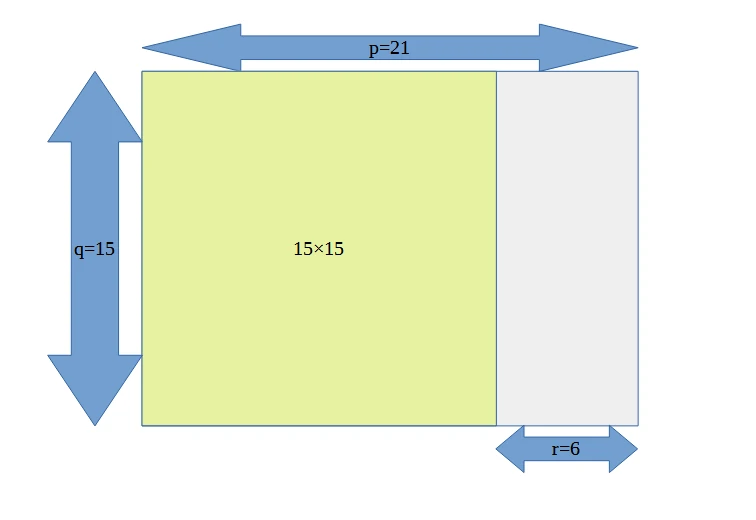
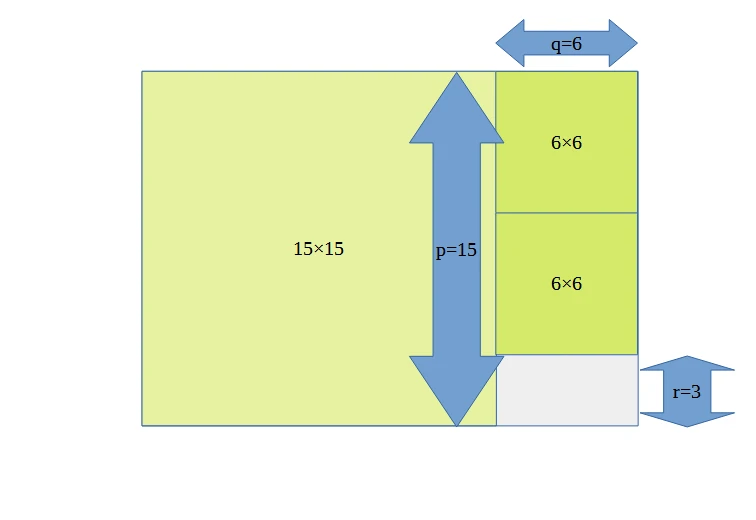
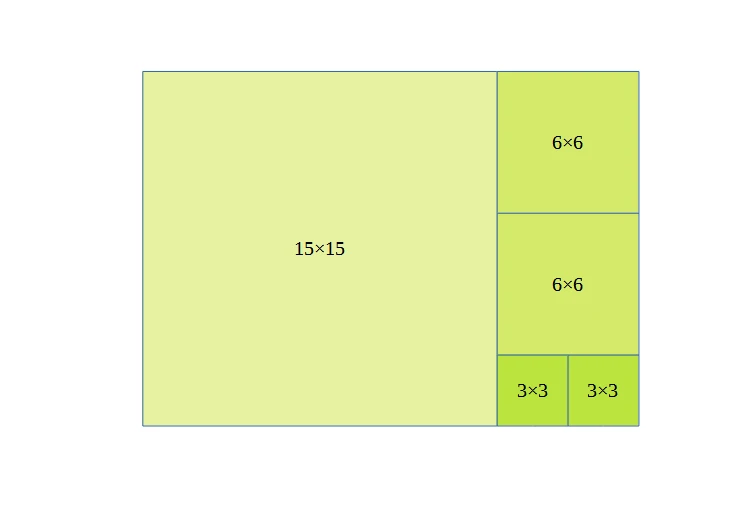
最終的に3×3の正方形が得られたので、長辺p、短辺qの長方形はこの正方形で埋めることができます。この正方形の辺の長さが最大公約数です。
ユークリッドの互除法の結果、最大公約数が1である場合もあります。例えば、195と154の最大公約数は1です。
| p | q | r | |
|---|---|---|---|
| 割り算1回目 | 195 | 154 | 41 |
| 割り算2回目 | 154 | 41 | 31 |
| 割り算3回目 | 41 | 31 | 10 |
| 割り算4回目 | 31 | 10 | 1 |
| 割り算5回目 | 10 | 1 | 0 |
自然数pとqの最大公約数が1の場合、pとqは互いに素であるといいます。上の例の場合、195と154は互いに素です。
do-whileでユークリッドの互除法を実装
Javaにはdo-while文という構文があります。(Javaの特有の構文ではありません。)今回はこの構文を使って、ユークリッドの互除法を実装しました。
do-while文の書き方は以下です。
do-while文
do {
[繰り返しのブロック]
} while ([条件]);[繰り返しのブロック]の箇所には繰り返したい処理を記述します。複数行を記述することが出来ます。
[条件]の箇所には条件式を記述することができます。
do-while文では次のように処理が実行されます。
- Step1:
- [繰り返しのブロック]を実行する。
- Step2:
- [条件]がtrueならば、Step1に戻る。
- それ以外ならば、処理を終える。
このように、do-while文の繰り返し処理は必ず1回実行されます。
上記構文を使い、以下のように、最大公約数を返却するメソッドを実装しました。
ソース
public class Test001 {
public static void main(String[] args) {
Test001 t = new Test001();
t.test(15, 21);
System.out.println("------------------");
t.test(154, 195);
}
private void test(int a, int b) {
System.out.println(a + "と" + b +"の最大公約数は" + gcdOf(a, b));
}
private int gcdOf(int a, int b) {
// (1)
int p;
int q = a;
int r = b;
// (2)
if (a < b) {
q = b;
r = a;
}
// (3)
do {
p = q;
q = r;
r = p % q;
} while (r > 0);
return q;
}
}結果
15と21の最大公約数は3
------------------
154と195の最大公約数は1上記サンプルのgcdOf()メソッドがユークリッドの互除法の実装例です。(メソッド名は最大公約数の英訳greatest common divisorを使いました。)int型変数aとbを引数にしています。返却する値はaとbの最大公約数です。なお、aとbには自然数が指定されると仮定しています。
(1)では計算のためのローカル変数を準備しています。
| 変数 | 値 |
|---|---|
| p | 0 |
| q | a |
| r | b |
仮引数のaとbをそれぞれqとrに代入しているのは、後のdo-while文の実行で値の入れ替え処理があるためです。(p ← q、q ← r。)
値の入れ替えをするため、変数pの初期値は意味がありません。そのため、明示的に初期化をする記述はしませんでした。(Java言語仕様のため、int型で宣言しているため、0が初期値として格納されます。)
(2)ではaの値の方がbより小さい場合の対処です。後のdo-while文でqの値をp、rの値をqに格納するときに、p \ge qになるように、if文で値を入れ替えてます。
(3)がユークリッドの互除法のアルゴリズムです。余りrが0より大きい場合、処理が繰り返されます。
do-while文の繰り返しが終了したとき、r=0です。そのため、最終的にqの値が最大公約数です。
途中経過を出力
do-while文の繰り返し処理で、変数の値がどのように変化しているか確認したいとします。
一番簡単な方法はprintln()で出力する方法ですが、今回はListの中に途中経過を格納するということをしてみました。
ソース
import java.util.ArrayList;
import java.util.Arrays;
public class Test002 {
private ArrayList<int[]> list;
public static void main(String[] args) {
Test002 t = new Test002();
t.test(15, 21);
System.out.println("------------------");
t.test(154, 195);
}
private void test(int a, int b) {
System.out.println(a + "と" + b +"の最大公約数は" + gcdOf(a, b));
// 追加(a)
for(int[] item : list) {
System.out.println(Arrays.toString(item));
}
}
private int gcdOf(int a, int b) {
// 追加(b)
list = new ArrayList<>();
// (1)
int p;
int q = a;
int r = b;
// (2)
if (a < b) {
q = b;
r = a;
}
// (3)
do {
p = q;
q = r;
r = p % q;
// 追加(c)
list.add(new int[] {p, q, r});
} while (r > 0);
return q;
}
}結果
15と21の最大公約数は3
[21, 15, 6]
[15, 6, 3]
[6, 3, 0]
------------------
154と195の最大公約数は1
[195, 154, 41]
[154, 41, 31]
[41, 31, 10]
[31, 10, 1]
[10, 1, 0]上記ではArrayList型の変数listをフィールドに定義しています。今回はint型配列を内容に持つArrayListを定義しています。リストに格納された順番に出力することが目的なので、ArrayListにしました。
追加(a)の箇所でArrayListの内容を出力しています。配列には以下のように値が格納されている想定です。
| 要素番号 | 値 |
|---|---|
| 0 | p |
| 1 | q |
| 2 | r |
Listの要素の出力は、拡張for文を使いました。サンプルのように記述す路と、変数itemにList内の配列が格納されます。
追加(b)の箇所では変数listにインスタンスを格納しています。gcdOf()メソッドが呼び出されると、listにインスタンスが格納されるという処理順序にしました。
追加(c)ではlistのadd()メソッドを使って、listに配列を格納しています。引数の箇所で、newと波括弧を使って、配列の初期化をしています。これは配列のイニシャライザーと呼ばれる初期化方法です。詳細は以下の記事で扱っています。
上記プログラムの出力結果をみると、p, q, rの値の経過が出力されています。値の入れ替えが想定通りになっていることがわかります。また、余りが最終的に0になっているのがわかります。
以上、参考になれば幸いです。